Trajectory inference for hematopoiesis in mouse

See also

More examples for trajectory inference on complex datasets can be found in the PAGA repository [Wolf et al., 2019], for instance, multi-resolution analyses of whole animals, such as for planaria for data of Plass et al. [2018].

Reconstructing myeloid and erythroid differentiation for data of Paul et al. (2015).

import numpy as np
import matplotlib.pyplot as pl
import scanpy as sc

sc.settings.verbosity = 3  # verbosity: errors (0), warnings (1), info (2), hints (3)
sc.logging.print_versions()
results_file = "./write/paul15.h5ad"
# low dpi (dots per inch) yields small inline figures
sc.settings.set_figure_params(dpi=80, frameon=False, figsize=(3, 3), facecolor="white")

scanpy==1.5.0 anndata==0.7.1 umap==0.4.2 numpy==1.18.1 scipy==1.4.1 pandas==1.0.3 scikit-learn==0.22.1 statsmodels==0.11.0

adata = sc.datasets.paul15()

WARNING: In Scanpy 0.*, this returned logarithmized data. Now it returns non-logarithmized data.

adata

AnnData object with n_obs × n_vars = 2730 × 3451 
    obs: 'paul15_clusters'
    uns: 'iroot'

Let us work with a higher precision than the default ‘float32’ to ensure exactly the same results across different computational platforms.

# this is not required and results will be comparable without it
adata.X = adata.X.astype("float64")

Preprocessing and Visualization

Apply a simple preprocessing recipe.

sc.pp.recipe_zheng17(adata)

running recipe zheng17
normalizing counts per cell
    finished (0:00:00)
extracting highly variable genes
    finished (0:00:00)
normalizing counts per cell
    finished (0:00:00)
    finished (0:00:00)

sc.tl.pca(adata, svd_solver="arpack")

computing PCA
    with n_comps=50
    finished (0:00:00)

sc.pp.neighbors(adata, n_neighbors=4, n_pcs=20)
sc.tl.draw_graph(adata)

computing neighbors
    using 'X_pca' with n_pcs = 20
    finished: added to `.uns['neighbors']`
    `.obsp['distances']`, distances for each pair of neighbors
    `.obsp['connectivities']`, weighted adjacency matrix (0:00:02)
drawing single-cell graph using layout 'fa'
    finished: added
    'X_draw_graph_fa', graph_drawing coordinates (adata.obsm) (0:00:14)

sc.pl.draw_graph(adata, color="paul15_clusters", legend_loc="on data")

This looks pretty messy.

Optional: Denoising the graph

To denoise the graph, we represent it in diffusion map space (and not in PCA space). Computing distances within a few diffusion components amounts to denoising the graph - we just take a few of the first spectral components. It’s very similar to denoising a data matrix using PCA. The approach has been used in a couple of papers, see e.g. Schiebinger et al. (2017) or Tabaka et al. (2018). It’s also related to the principles behind MAGIC Dijk et al. (2018).

Note

This is not a necessary step, neither for PAGA, nor clustering, nor pseudotime estimation. You might just as well go ahead with a non-denoised graph. In many situations (also here), this will give you very decent results.

sc.tl.diffmap(adata)
sc.pp.neighbors(adata, n_neighbors=10, use_rep="X_diffmap")

computing Diffusion Maps using n_comps=15(=n_dcs)
computing transitions
    finished (0:00:00)
    eigenvalues of transition matrix
    [1.         1.         0.9989278  0.99671    0.99430376 0.98939794
     0.9883687  0.98731077 0.98398703 0.983007   0.9790806  0.9762548
     0.9744365  0.9729161  0.9652972 ]
    finished: added
    'X_diffmap', diffmap coordinates (adata.obsm)
    'diffmap_evals', eigenvalues of transition matrix (adata.uns) (0:00:00)
computing neighbors
    finished: added to `.uns['neighbors']`
    `.obsp['distances']`, distances for each pair of neighbors
    `.obsp['connectivities']`, weighted adjacency matrix (0:00:00)

sc.tl.draw_graph(adata)

drawing single-cell graph using layout 'fa'
    finished: added
    'X_draw_graph_fa', graph_drawing coordinates (adata.obsm) (0:00:13)

sc.pl.draw_graph(adata, color="paul15_clusters", legend_loc="on data")

This still looks messy, but in a different way: a lot of the branches are overplotted.

Clustering and PAGA

Note

Note that today, we’d use sc.tl.leiden - here, we use sc.tl.louvain the sake of reproducing the paper results.

sc.tl.louvain(adata, resolution=1.0)

running Louvain clustering
    using the "louvain" package of Traag (2017)
    finished: found 25 clusters and added
    'louvain', the cluster labels (adata.obs, categorical) (0:00:00)

Annotate the clusters using marker genes.

cell type	marker
HSCs	Procr
Erythroids	Gata1, Klf1, Epor, Gypa, Hba-a2, Hba-a1, Spi1
Neutrophils	Elane, Cebpe, Ctsg, Mpo, Gfi1
Monocytes	Irf8, Csf1r, Ctsg, Mpo
Megakaryocytes	Itga2b (encodes protein CD41), Pbx1, Sdpr, Vwf
Basophils	Mcpt8, Prss34
B cells	Cd19, Vpreb2, Cd79a
Mast cells	Cma1, Gzmb, CD117/C-Kit
Mast cells & Basophils	Ms4a2, Fcer1a, Cpa3, CD203c (human)

For simple, coarse-grained visualization, compute the PAGA graph, a coarse-grained and simplified (abstracted) graph. Non-significant edges in the coarse- grained graph are thresholded away.

sc.tl.paga(adata, groups="louvain")

running PAGA
    finished: added
    'paga/connectivities', connectivities adjacency (adata.uns)
    'paga/connectivities_tree', connectivities subtree (adata.uns) (0:00:00)

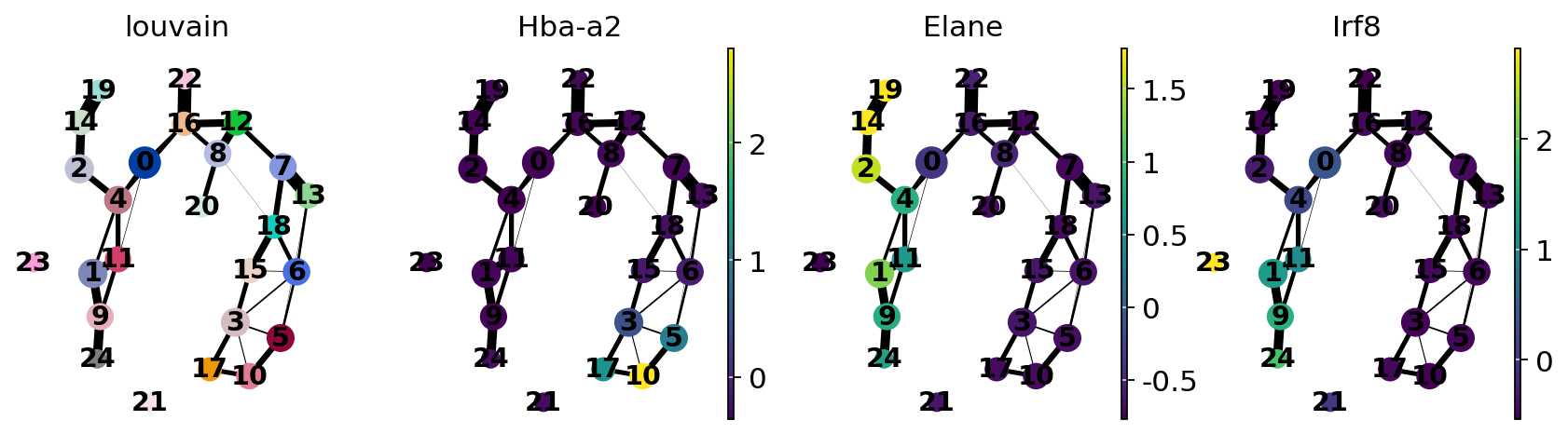
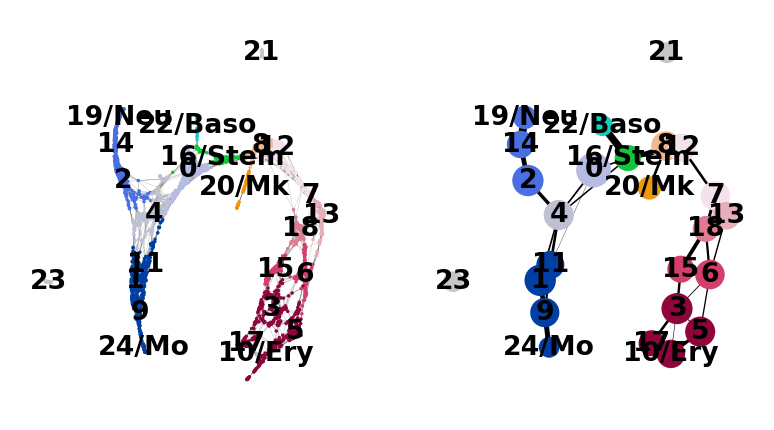
sc.pl.paga(adata, color=["louvain", "Hba-a2", "Elane", "Irf8"])

--> added 'pos', the PAGA positions (adata.uns['paga'])

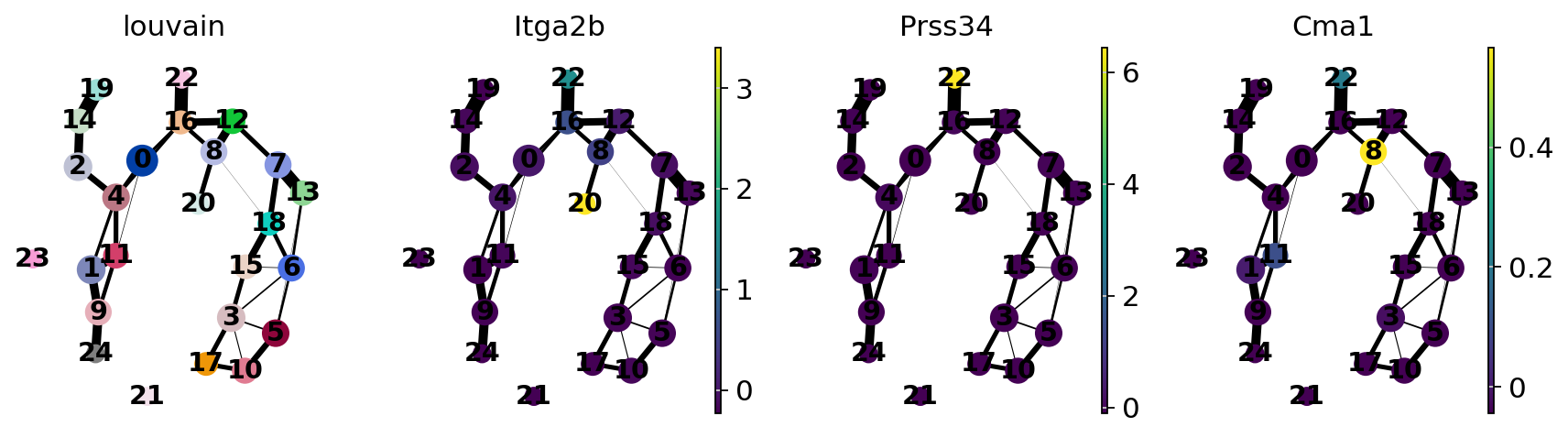
sc.pl.paga(adata, color=["louvain", "Itga2b", "Prss34", "Cma1"])

--> added 'pos', the PAGA positions (adata.uns['paga'])

Actually annotate the clusters — note that Cma1 is a Mast cell marker and only appears in a small fraction of the cells in the progenitor/stem cell cluster 8, see the single-cell resolved plot below.

adata.obs["louvain"].cat.categories

Index(['0', '1', '2', '3', '4', '5', '6', '7', '8', '9', '10', '11', '12',
       '13', '14', '15', '16', '17', '18', '19', '20', '21', '22', '23', '24'],
      dtype='object')

adata.obs["louvain_anno"] = adata.obs["louvain"]

adata.obs["louvain_anno"].cat.categories = [
    *["0", "1", "2", "3", "4", "5", "6", "7", "8", "9"],
    *["10/Ery", "11", "12", "13", "14", "15"],
    *["16/Stem", "17", "18"],
    *[
        "19/Neu",
        "20/Mk",
        "21",
    ],
    *["22/Baso", "23", "24/Mo"],
]

Let’s use the annotated clusters for PAGA.

sc.tl.paga(adata, groups="louvain_anno")

running PAGA
    finished: added
    'paga/connectivities', connectivities adjacency (adata.uns)
    'paga/connectivities_tree', connectivities subtree (adata.uns) (0:00:00)

sc.pl.paga(adata, threshold=0.03, show=False)

--> added 'pos', the PAGA positions (adata.uns['paga'])

<matplotlib.axes._axes.Axes at 0x7fbbfcccf690>

Recomputing the embedding using PAGA-initialization

The following is just as well possible for a UMAP.

sc.tl.draw_graph(adata, init_pos="paga")

drawing single-cell graph using layout 'fa'
    finished: added
    'X_draw_graph_fa', graph_drawing coordinates (adata.obsm) (0:00:13)

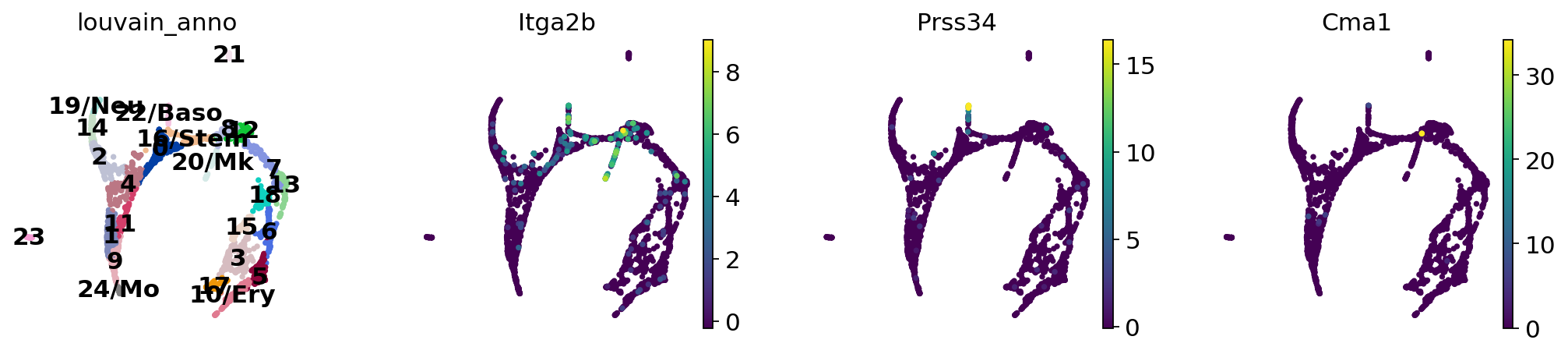
Now we can see all marker genes also at single-cell resolution in a meaningful layout.

sc.pl.draw_graph(
    adata, color=["louvain_anno", "Itga2b", "Prss34", "Cma1"], legend_loc="on data"
)

Choose the colors of the clusters a bit more consistently.

pl.figure(figsize=(8, 2))
for i in range(28):
    pl.scatter(i, 1, c=sc.pl.palettes.zeileis_28[i], s=200)
pl.show()

zeileis_colors = np.array(sc.pl.palettes.zeileis_28)
new_colors = np.array(adata.uns["louvain_anno_colors"])

new_colors[[16]] = zeileis_colors[[12]]  # Stem colors / green
new_colors[[10, 17, 5, 3, 15, 6, 18, 13, 7, 12]] = zeileis_colors[  # Ery colors / red
    [5, 5, 5, 5, 11, 11, 10, 9, 21, 21]
]
new_colors[[20, 8]] = zeileis_colors[[17, 16]]  # Mk early Ery colors / yellow
new_colors[[4, 0]] = zeileis_colors[[2, 8]]  # lymph progenitors / grey
new_colors[[22]] = zeileis_colors[[18]]  # Baso / turquoise
new_colors[[19, 14, 2]] = zeileis_colors[[6, 6, 6]]  # Neu / light blue
new_colors[[24, 9, 1, 11]] = zeileis_colors[[0, 0, 0, 0]]  # Mo / dark blue
new_colors[[21, 23]] = zeileis_colors[[25, 25]]  # outliers / grey

adata.uns["louvain_anno_colors"] = new_colors

And add some white space to some cluster names. The layout shown here differs from the one in the paper, which can be found here. These differences, however, are only cosmetic. We had to change the layout as we moved from a randomized PCA and float32 to float64 precision.

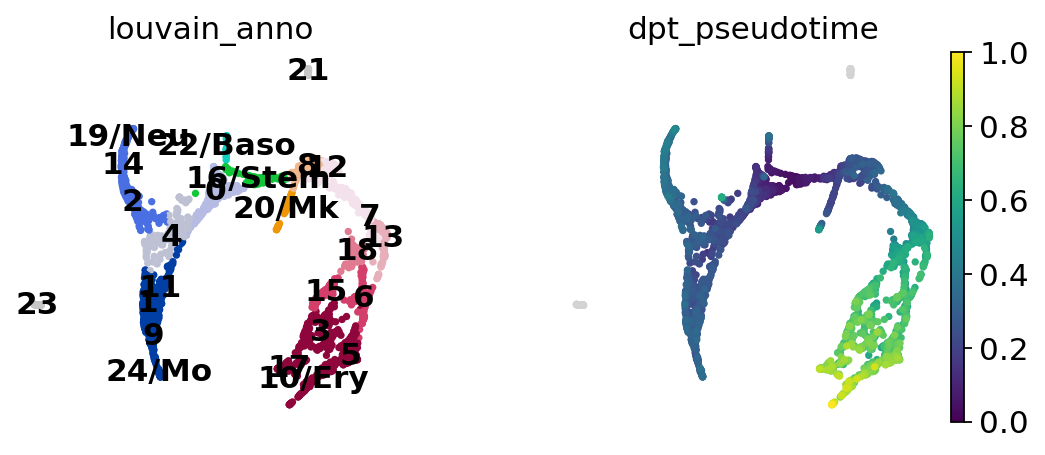
sc.pl.paga_compare(
    adata,
    threshold=0.03,
    title="",
    right_margin=0.2,
    size=10,
    edge_width_scale=0.5,
    legend_fontsize=12,
    fontsize=12,
    frameon=False,
    edges=True,
    save=True,
)

--> added 'pos', the PAGA positions (adata.uns['paga'])
WARNING: saving figure to file figures/paga_compare.pdf

Reconstructing gene changes along PAGA paths for a given set of genes

Choose a root cell for diffusion pseudotime.

adata.uns["iroot"] = np.flatnonzero(adata.obs["louvain_anno"] == "16/Stem")[0]

sc.tl.dpt(adata)

computing Diffusion Pseudotime using n_dcs=10
    finished: added
    'dpt_pseudotime', the pseudotime (adata.obs) (0:00:00)

Select some of the marker gene names.

gene_names = [
    *["Gata2", "Gata1", "Klf1", "Epor", "Hba-a2"],  # erythroid
    *["Elane", "Cebpe", "Gfi1"],  # neutrophil
    *["Irf8", "Csf1r", "Ctsg"],  # monocyte
]

Use the full raw data for visualization.

adata_raw = sc.datasets.paul15()
sc.pp.log1p(adata_raw)
sc.pp.scale(adata_raw)
adata.raw = adata_raw

WARNING: In Scanpy 0.*, this returned logarithmized data. Now it returns non-logarithmized data.

sc.pl.draw_graph(adata, color=["louvain_anno", "dpt_pseudotime"], legend_loc="on data")

paths = [
    ("erythrocytes", [16, 12, 7, 13, 18, 6, 5, 10]),
    ("neutrophils", [16, 0, 4, 2, 14, 19]),
    ("monocytes", [16, 0, 4, 11, 1, 9, 24]),
]

adata.obs["distance"] = adata.obs["dpt_pseudotime"]

adata.obs["clusters"] = adata.obs["louvain_anno"]  # just a cosmetic change

adata.uns["clusters_colors"] = adata.uns["louvain_anno_colors"]

!mkdir write

mkdir: cannot create directory ‘write’: File exists

_, axs = pl.subplots(
    ncols=3, figsize=(6, 2.5), gridspec_kw={"wspace": 0.05, "left": 0.12}
)
pl.subplots_adjust(left=0.05, right=0.98, top=0.82, bottom=0.2)
for ipath, (descr, path) in enumerate(paths):
    _, data = sc.pl.paga_path(
        adata,
        path,
        gene_names,
        show_node_names=False,
        ax=axs[ipath],
        ytick_fontsize=12,
        left_margin=0.15,
        n_avg=50,
        annotations=["distance"],
        show_yticks=True if ipath == 0 else False,
        show_colorbar=False,
        color_map="Greys",
        groups_key="clusters",
        color_maps_annotations={"distance": "viridis"},
        title="{} path".format(descr),
        return_data=True,
        show=False,
    )
    data.to_csv("./write/paga_path_{}.csv".format(descr))
pl.savefig("./figures/paga_path_paul15.pdf")
pl.show()